この記事のねらい
この記事では論理的帰結と証明可能性について定義します.
論理的帰結の定義
論理的帰結とはなにかということを明確にするときに,論理的とはなにかということから考えることは少し遠回りです.
ここで知りたいのは帰結でありゴールの方です.したがって,論理的帰結であると言える時に結局何が成り立っていればよいのかだけに注目します.
そこで,論理式\( \varphi \)が論理式の集合\( \Gamma \)を満たす任意のモデルで正しくなることだけを要求します.
これはまさに現代確率論がランダムとは何かに触れることなく確率変数を定義することに成功したように,論理的とは何かという問題に触れずに論理的帰結であることだけを定義しています.それがモデルを用いた強みです.
定義(論理的帰結):
論理式の集合を\( \Gamma \)とし, \( \varphi \)を論理式とする.
\( \Gamma \)を充足する任意の付値\( \nu \)が\( \nu(\varphi) = 1 \)を満たすとき,\( \Gamma \vDash \varphi \)と表し\( \varphi \)は\( \Gamma \)の論理的帰結であるという.
見やすくまとめましょう.
\( \Gamma \vDash \varphi :\Leftrightarrow\) \( \Gamma \)を充足する任意の付値\( \nu \)について\( \nu( \varphi ) = 1 \)が成り立つ.
さて,上記の定義で\( \Gamma \)は集合としましたから空集合でもよいことになります.\( \Gamma = \emptyset \)のとき\(\Gamma\)を省略して\( \vDash \varphi \)と表します.これは全くなんの条件も仮定せずとも\(\varphi\)は正しいことがわかってしまうということです.このような\(\varphi\)には特別な名前があります.
定義(トートロジー):
\( \vDash \varphi \)となる論理式\( \varphi \)をトートロジーという.
たとえば,\( \lnot \varphi \lor \varphi \)はトートロジーです.任意の付値\( \nu \)について,
\( \nu(\lnot \varphi \lor \varphi) = {\rm max}(1 – \nu(\varphi), \nu(\varphi)), \)
となりますが明らかに\(1 – \nu(\varphi), \nu(\varphi) \)のどちらかは\(1\)です.
形式的証明の定義
形式的証明を定義するのは証明可能性を定義するためです.数理論理学の目的の1つは証明できることと論理的帰結であることが同値になることを数学的に示すことです.
そのためには証明とはなにかをはっきり定義し,証明可能とはなにかを定義する必要があります.
議論の見通しをよくするために,証明論においては論理記号は\( \bot, \rightarrow \)のみとします.このとき,論理式\( \varphi, \psi \)について,
\( \lnot \varphi := \varphi \rightarrow \bot, \)
\( \varphi \lor \psi := \lnot \varphi \rightarrow \psi, \)
\( \varphi \land \psi := \lnot ( \varphi \rightarrow \lnot \psi ), \)
と定めます.こうしておくことで,公理も減りますし演繹定理の時に示さなければならないことも減ります.
定義(証明系\( \mathcal{H} \)):
公理:
(1) \( \varphi \rightarrow \psi \rightarrow \varphi, \)
(2) \( (\varphi \rightarrow \psi \rightarrow \theta) \rightarrow ( \varphi \rightarrow \psi) \rightarrow \varphi \rightarrow \theta, \)
(3) \( \lnot \lnot \varphi \rightarrow \varphi. \)
推論規則:
(MP) \( \frac{\varphi \rightarrow \psi \quad \varphi}{\psi} \).
(MP)はモーダスポネンスの略です.ここで公理はすべてトートロジーになっていることを注意しておきます.
また,モーダスポネンスが正しさを保存する推論であることを確認しておきます.
命題3-1:
\( \{ \varphi \rightarrow \psi, \varphi\} \vDash \psi, \)
(証明)
\( \{ \varphi \rightarrow \psi, \varphi\} \)を満たす任意の付値を\(\nu\)とする.このとき,
\( \nu(\varphi \rightarrow \psi) = {\rm max}(1 – \nu(\varphi), \nu(\psi)) = 1, \)
\( \nu(\varphi) = 1, \)
が共に成り立つ.よって,\( 1 – \nu(\varphi) = 0 \)より\( \nu(\psi) = 1 \)でなくてはならない.
最後に証明可能性を定義しましょう.
定義(証明・証明可能):
論理式の集合を\( \Gamma \)とする.証明系\( \mathcal{H} \)における証明とは論理式の有限列,
\( \quad \varphi_1, \varphi_2, \cdots, \varphi_n, \)
で\( \varphi_n = \varphi \)であり, \( \varphi_i \: (i = 1, 2, \cdots, n-1)\)は\( \Gamma \)の元であるか\( \mathcal{H} \)の公理であるか\( j, k < i\)なる\(\varphi_j, \varphi_k\)からの推論規則(MP)による結論となっているようなものである.
また,\( \Gamma \)からの\( \varphi \)の証明が存在するとき\( \varphi \)は\( \Gamma \)から証明可能といい,\( \Gamma \vdash \varphi \) と表す.
ここでのポイントは証明は論理式の有限列だということです.ある論理式が証明できるときは必ず有限個の論理式から導けるということです.
実はこれは重要な性質で論理的帰結の場合には定義からは成り立つか不明な事実です(あとで成り立つことがわかるのですが). つまり,有限でない\(\Gamma\)について\( \Gamma \vDash \varphi\)となっているとき,有限部分集合\(\Gamma_0 \subset \Gamma\)をとって\( \Gamma_0 \vDash \varphi\)とできるかは直ちにはわかりません.
それはさておき,ひとまずこれで証明可能性を定義することができました.
また,トートロジーと同様に何も仮定せずに証明できる論理式は次のように表します.
\( \Gamma \)が空集合のとき, \( \Gamma \vdash \varphi \)を\(\vdash \varphi \)と表す.
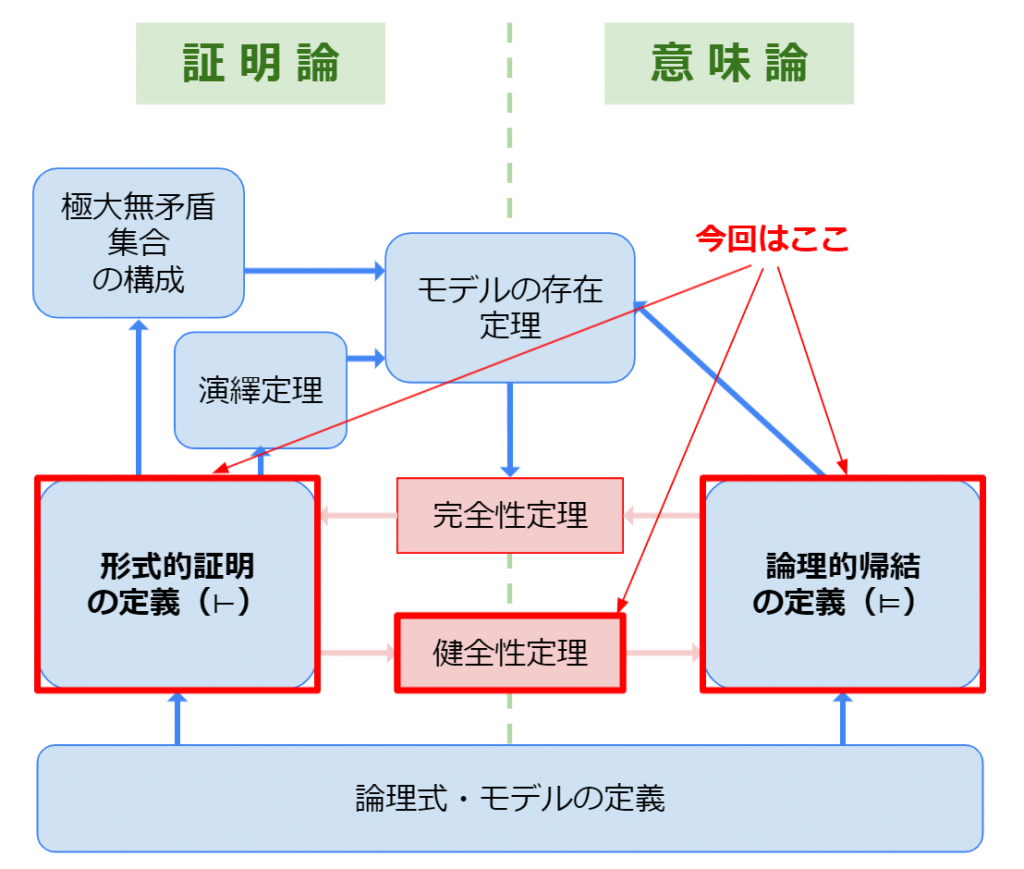
健全性定理
ここまでの議論で赤枠の定理の下側,健全性定理が示せます.なぜならば\( \mathcal{H}\)の公理がすべてトートロジーであり(MP)が正しさを保存する推論である以上,証明可能であれば論理的帰結であると言えるからです.
定理(健全性定理):
\( \Gamma \vdash \varphi \Rightarrow \Gamma \vDash \varphi \)
さて,次回以降はこの定理の逆,完全性定理に向かって進んでいきます.
完全性は健全性と違って自明ではありません.健全性については正しさを保存してくれるように証明を作ったので言ってしまえば成り立って当然です.一方の完全性は正しい結論は必ず証明できるという内容です.
これは証明が十分な表現力を持っていることを示す定理であり,非常に重要な定理です.それでは,また次回.
参考文献
[1] 新井敏康,数学基礎論 増補版,東京大学出版会,2021.
[2] ケネス・キューネン, キューネン数学基礎論講義, 日本評論社,2016.
[3] 鹿島亮, 現代基礎数学15 数理論理学, 朝倉書店, 2009.