数理論理学とは
数理論理学は数学の一分野です。
以前、数学が専門ではなかったけどこのブログを覗いてくださっているという方に「何をやっているのかわからない」というお声をいただきました。
たしかに分野外の方のために少なくとも何をやっているのかがわかるような記事も1つは書かなくてはと思い、本記事を書いています。
数理論理学は数学であって哲学でないということは強調しておかなくてはなりません。
ただし、数学における研究結果から哲学分野の人々が何かを読み取るということは可能だと思います。それに、ぼく自身哲学的に数学を捉えることにはすごく関心があり、問題意識は多少哲学と重なっていると感じます。
実際、ゲーデルの不完全性定理は良くも悪くも哲学分野に影響を与えたようです(誤った解釈もかなり多かったようですが)。
ただし、数理論理学における手法も諸結果もあくまで数学であるということがポイントです。
言いたいことは数理論理学は数学の一分野だということです。
なぜそんなことをするのか(歴史的経緯)
高校一年生の頃に集合というものを習ったのは覚えていますか? 高校では深くやりませんが、実は集合論は現代数学にとって非常に重要な存在です。
今からちょうど100年ほど前に、その集合論にパラドックス(=矛盾)が見つかりました。それは自身を含まない集合全体の集合を考えると矛盾が生じるというものでした。
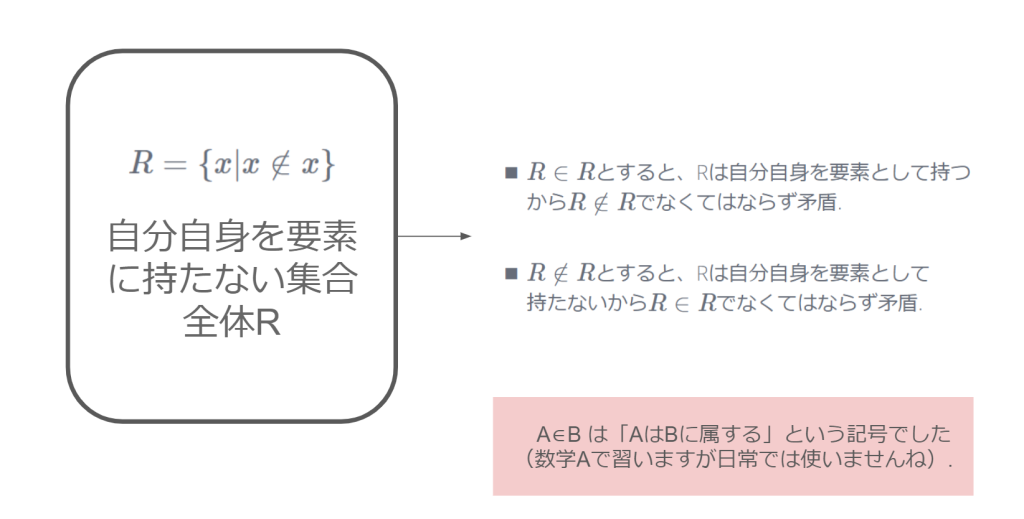
当時、カントールからはじまりヒルベルトの活躍が後押しして数学の多くの分野が集合論の言葉でうまく表現できることが知られていました。
その集合論で矛盾が生じるということは数学が矛盾しているということになります。
当然数学者は数学が矛盾していてほしくないので、集合論を公理化する(ZFC公理系)ことで厳密に表現し、矛盾を解消することを目指しました。
簡単に言うと、矛盾を生じさせるような集合を排除するように公理系を設計することで矛盾を解消しました(別の回避方法もいくつか提案されています)。
ZFC公理系でひとまず目の前にあった矛盾は回避したわけですが、再び致命的な矛盾が見つからないとも限りません。
そこで、その公理系が無矛盾であることを示そうという試みがなされました。
そうして始まったのが数理論理学であり、数学基礎論です。日本語の数理論理学・数学基礎論はほとんど同じ意味で使われます。
結局、数学は無矛盾か
ひとまず、数学の無矛盾性を示したいという大目標は立ったわけですが、結局この目標はどうなったのでしょうか。
もったいぶらずにオチをいってしまいますが、公理によって数学を表現する方法では数学の無矛盾性は示せませんでした。
というか、多くの公理系でその公理系自身の無矛盾性を証明することは決してできないということが証明されました。
つまり、ZFC公理系の無矛盾性もZFC公理系だけを使って示すことはできませんでした。
これが比較的有名なゲーデルの不完全性定理です。
大数学者であり当時の数学会を牽引する存在であったヒルベルトですらこの方法で無矛盾性を証明できると信じていたので、当時の数学会では一大ニュースであったことと思います。
数理論理学の魅力
しかし、ある公理系\(T\)が\(T\)自身の無矛盾性を証明できないとしても、\(T\)に何かを付け加えた\(T’\)という公理系では\(T\)の無矛盾性を証明できることがあります。
そうすると、\(T’\)は\(T\)の無矛盾性を証明できるという意味で\(T\)よりも真に強い理論であることがわかります。
このように、ゲーデルの不完全性定理によってはじめて展開できる数学があることも分かりました。
数理論理学の魅力はここで紹介しつくすにはとてもスペースが足りませんが、ひとまず歴史的に意義深い分野であることは伝わったかと思います。
これからも専門外の方にも面白さが伝わるような記事が書ければよいなと思います。