今回の内容
今回はこの範囲です.
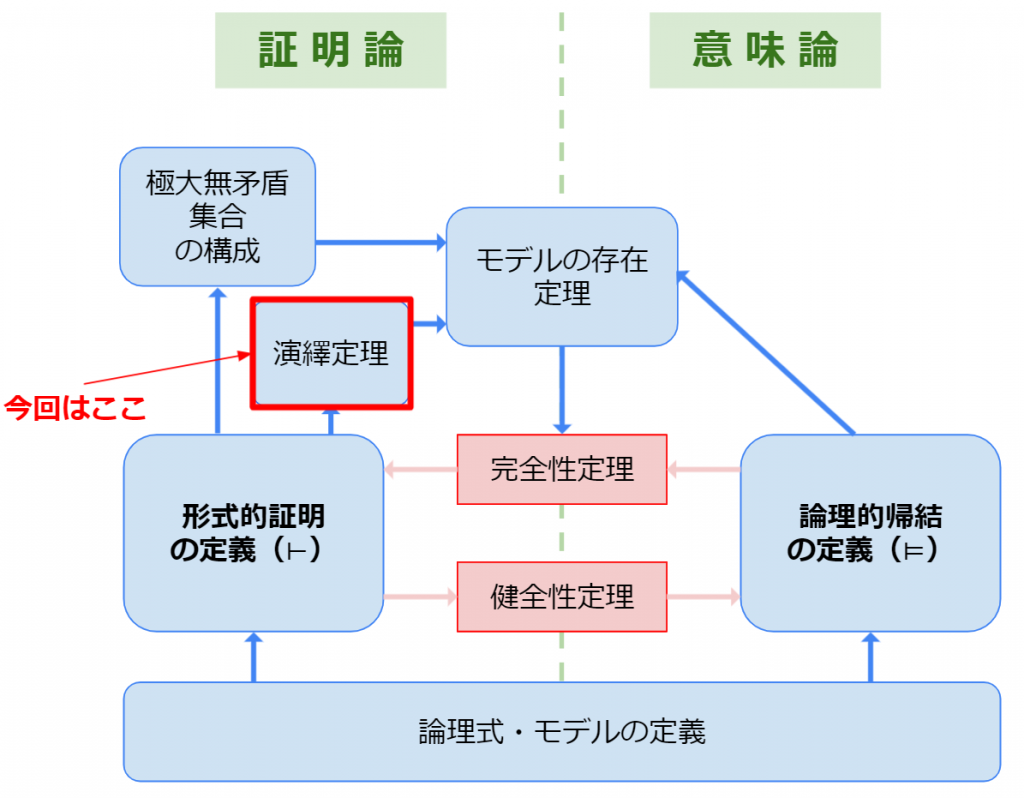
演繹定理
形式的証明系がどのような定理を証明できるか調べる際に演繹定理は非常に有益な定理です.
あまりくどくど説明せず,ステートメントを述べます.
定理(演繹定理):
\( \Gamma \)を論理式の集合とする.このとき,次が成り立つ.
\( \Gamma \vdash \varphi \rightarrow \psi \iff \Gamma \cup \{ \varphi \} \vdash \psi \).
(証明)
( \(\Longrightarrow\) )
\( \Gamma \vdash \varphi \rightarrow \psi \)かつ\( \Gamma \subset \Gamma \cup \{ \varphi \} \)より,\( \Gamma \cup \{ \varphi \} \vdash \varphi \rightarrow \psi \)が成り立つ.よって,(MP)より\( \Gamma \cup \{ \varphi \} \vdash \psi \).
( \(\Longleftarrow\) )
\( \psi \)の種類によって場合分けする.
[1] \( \psi \in \Gamma \)のとき.\( \mathcal{H} \)の公理(1)より\( \Gamma \vdash \psi \rightarrow \varphi \rightarrow \psi \)であり,これと\( \psi \)で(MP)を使うことで\( \Gamma \vdash \varphi \rightarrow \psi \)を得る(注:\(\psi \rightarrow \varphi \rightarrow \psi \)とは\( \psi \rightarrow (\varphi \rightarrow \psi) \)を表すのであった).
[2] \( \psi\)が\( \mathcal{H} \)の公理のとき.\( \Gamma \vdash \psi \)および\( \mathcal{H} \)の公理(1)より\( \Gamma \vdash \psi \rightarrow \varphi \rightarrow \psi \)より(MP)を使えば\( \Gamma \vdash \varphi \rightarrow \psi \)を得る.
[3] \( \psi \equiv \varphi \)のとき. 次の補題4-1で示す.
[4] \( \psi\)が(MP)の結論になっているとき.\( \Gamma \cup \{ \varphi \} \)からの\( \psi \)の証明の長さに関する帰納法で示す.長さ\(1\)の時は[1]~[3]の場合に相当するから示された.証明の長さが\(n\)のとき,ある論理式\(\theta\)について\( \Gamma \cup \{ \varphi \} \vdash \theta \rightarrow \psi \)および\( \Gamma \cup \{ \varphi \} \vdash \theta \)が成り立っているから帰納法の仮定より,\( \Gamma \vdash \varphi \rightarrow \theta \rightarrow \psi \)および\( \Gamma \vdash \varphi \rightarrow \theta \)を得る. \( \mathcal{H} \)の公理(2)より, \( \Gamma \vdash (\varphi \rightarrow \theta \rightarrow \psi) \rightarrow (\varphi \rightarrow \theta) \rightarrow \varphi \rightarrow \psi \)が成り立つから(MP)を2回用いることで結論を得る.
補題4-1:
\( \vdash \varphi \rightarrow \varphi \).
(証明)
\( \theta = \varphi \rightarrow \varphi \)とする.\(\mathcal{H}\)の公理(2)より,
\( \vdash (\varphi \rightarrow \theta \rightarrow \varphi) \rightarrow (\varphi \rightarrow \theta) \rightarrow \varphi \rightarrow \varphi, \)
が成り立つ.また,\(\mathcal{H}\)の公理(1)より, \( \vdash \varphi \rightarrow \theta \rightarrow \varphi, \vdash \varphi \rightarrow \varphi \rightarrow \varphi \)が成り立つから(MP)を2回使えばよい.
証明系\( \mathcal{H} \)の公理はもっと多く仮定されてある本が少なくないです.このブログ記事は参考文献として新井敏康先生の数学基礎論を主に使用しています.筆者がこの本の完全性の証明が好きなのは公理系の少なさにあります.命題論理だけなら公理3つ推論規則1つで完全性が示せてしまいます.すっきりしていてシンプルです.
ただ,純モデル論的な帰結であるコンパクト性定理をモデル論の範囲だけで示したかったのか,極大無矛盾集合の構成を新井本では使いません(極大集合とでもいうべき似た手法,しかし論理的帰結さえ定義できていれば使える手法でコンパクト性を示しています).
この連載では極大無矛盾集合という証明論を用いた手法で完全性を示します.つまり,モデルの存在定理を示してから完全性を示す方法です.キューネンの本や鹿島亮先生の本で用いられる手法です.
こうして両者のいいとこ取りをして,命題論理全体をすっきり理解することを目指します.
ということで,次回はいよいよ完全性定理です.
おまけ:演繹定理の応用
演繹定理は実際に自分で手を動かしてみるとありがたさがわかります.
たとえば,次のような命題を楽に示すことができます.
命題4-2:
\( \vdash \varphi \rightarrow \lnot \lnot \varphi\).
これは\(\mathcal{H}\)の公理(3)の逆である.よって,これより\( \varphi \)を示すことと\( \lnot \lnot \varphi \)を示すことは同値であることがわかる.
(証明)
\( \{ \varphi \} \vdash \lnot \lnot \varphi \)
\( \quad \iff \{ \varphi \} \vdash \lnot \varphi \rightarrow \bot \)
\( \quad \iff \{ \varphi, \lnot \varphi \} \vdash \bot \)
\( \quad \iff \{ \lnot \varphi \} \vdash \varphi \rightarrow \bot \)
\( \quad \iff \vdash \lnot \varphi \rightarrow \lnot \varphi \).
最後の形は補題4-1より成り立つため,証明された.
この他にもいろいろなことを示せます. 証明論の命題を示したくて迷ったら演繹定理を使ってみるとできるかもと考えることは有益だと思います.
参考文献
[1] 新井敏康,数学基礎論 増補版,東京大学出版会,2021.
[2] ケネス・キューネン, キューネン数学基礎論講義, 日本評論社,2016.
[3] 鹿島亮, 現代基礎数学15 数理論理学, 朝倉書店, 2009.